Page 3
A Consensus Cladogram
Page 3
A Consensus Cladogram

The following is a very concise explanantion from the PAUPDISPLAY Manual:
* strict consensus. A strict consensus tree groups sequences only if that grouping appears in all of the trees. For many sets of trees, this method is too strict. For example, two trees may be identical except for the placement of a single sequence, yet their strict consensus tree might be completely unresolved (a star phylogeny). Strict consensus trees are the easiest type to interpret -- if a group appears in the consensus tree, it appears in all of the trees of the set.
* semistrict consensus. This method is also called "combinable component" consensus. If a particular grouping in one tree is not contradicted by the other trees, it will be retained in the consensus. For example, if all trees have either an (A,B,C) trichotomy or an ((A,B),C) dichotomy, then the consensus will have the group (A,B) since this grouping is not contradicted by the (A,B,C) trichotomy. When there is a conflict in grouping, semistrict consensus behaves like strict consensus.
* majority-rule consensus. This method allows a group to appear in the consensus even if some of the trees in the set contradict it, as long as a (pre-specified) majority of the trees support the grouping. Typically, the majority is considered to be more than 50 percent of the trees in the set. When comparing only two trees, this method is equivalent to the strict consensus method.
* Adams consensus. This method is based on the idea that a tree
should be thought of as a "set of leaf subset nestings" rather than as
a "set of clusters." A group nests within a larger group if the most recent
common ancestor of the smaller group is a descendant of the most recent
common ancestor of the larger group. Because the Adams method needs to
know ancestor-descendant relationships, it can only be used for rooted
trees. An advantage of this method is that it often preserves more structure
than the strict methods. A drawback is that it may show groups in the consensus
tree that do not occur in any of the trees in the set, which makes interpretation
of the consensus tree somewhat more difficult. For example, the Adams consensus
tree for (A,(((B,E),C),D)) and (A,(((B,D),C),E)) is (A,(B,C),D,E). The
(B,C) grouping in this Adams consensus tree means only that B and C are
more closely related to each other than either is to A, D, or E. (The strict
consensus tree for these two trees would be the completely unresolved tree
(A,B,C,D,E).)
What defines a clade and makes it defensible?
SYNAPOMORPHY
MONOPHYLY
Other Considerations
Tree and Character Measures
CI (chars/changes) *if all binary*
RI (changes/maximum possible)
HRS ((1/CI-1)/t-3))/H
H being a predicted homoplasy level for randomized data of the set
size specified. See table in:
Meier et al. 1991. Homoplasy slope ratio: a better measurement of observed
homoplasy in cladistic analyses. Systematic Zoology 40: 74-88.
Bootstrap
Long Branches
ACCTRAN vs. DELTRAN
Favoring reversals or parallelisms
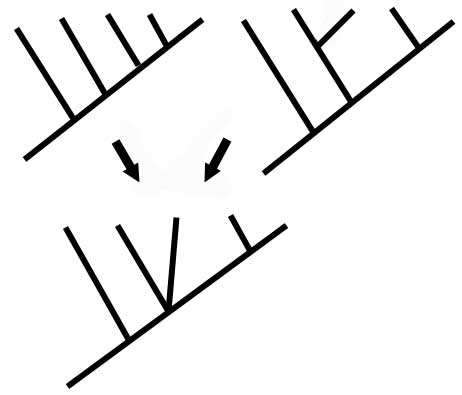
Just a final note: remember that a cladogram is simply a schematic representation of a network, thus, all of the cladograms below are the same.
LINKS